29.

PIERŚCIENIE GĘSTOŚCI*

...we wzorcu EKSCENTRYCZNE JĄDRO (28) przedstawiliśmy ogólny schemat konfiguracji „szczytów” i „dolin gęstości”, uwzględniający MOZAIKĘ PODKULTUR (8) i GRANICĘ PODKULTURY (13). Przypuśćmy teraz, że centrum aktywności handlowej w SIEDMIOTYSIĘCZNEJ SPOŁECZNOŚCI (12) zbudowano zgodnie z zaleceniami wzorca EKSCENTRYCZNE JĄDRO (28) oraz stosownie do ogólnej gęstości w tej części miasta. Pojawia się problem ustalenia lokalnych gęstości dla zgrupowań domów mieszkalnych i zakładów pracy znajdujących się w różnych odległościach od tego szczytu. Niniejszy wzorzec przedstawia zasadę, zgodnie z którą można opracować gradient tych lokalnych gęstości. A konkretnie, gradient ten można określić, rysując pierścienie w różnych odległościach od głównego centrum aktywności, i następnie przypisując różne gęstości każdemu z pierścieni. W ten sposób zróżnicowane wartości występujące w kolejnych pierścieniach dadzą w rezultacie gradient intensywności, który będzie różny dla różnych społeczności, zarówno w zależności od usytuowania terenu zamieszkanego przez daną społeczność w regionie, jak i od jej uwarunkowań kulturowych.

***

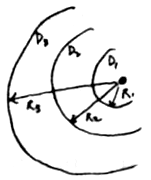
  Ludzie dla rozrywki i wygody chcą mieszkać niedaleko sklepów i innych usług. Jednak zarazem chcą być daleko od tych usług, dążąc do zacisza i zieleni. Punkt równowagi między tymi dwoma pragnieniami zależy od danego człowieka. W całości jednak to właśnie ta równowaga przeciwstawnych pragnień determinuje gradient gęstości zabudowy mieszkaniowej w danym sąsiedztwie.
  Żeby zachować precyzję w związku z gradientem gęstości zabudowy mieszkaniowej, ustalmy od razu, że gęstości te będziemy analizować, stosując trzy półkoliste, współśrodkowe pierścienie o jednakowej miąższości (szerokości promieniowej).
  Używamy półokręgów zamiast pełnych okręgów, ponieważ wykazano empirycznie, że obszar zbiorczy danego lokalnego centrum po stronie oddalonej od centrum miasta ma kształt półokręgu wspominaliśmy o tym już we wzorcu EKSCENTRYCZNE JĄDRO (28). Zainteresowanym polecamy także prace Brennana i Lee, do których odwołujemy się w tym wzorcu. Jednakże, nawet jeśli się nie zgadzasz z tymi wnioskami i wolisz uważać, że są to pełne okręgi, poniższa analiza pozostaje zasadniczo bez zmian.
Pierścienie o jednakowej miąższości
  Teraz możemy definiować gradient gęstości jako układ trzech różnych gęstości charakterystycznych dla każdego z pierścieni.
Gradient gęstości
  Wyobraźmy sobie, że trzy pierścienie jakiegoś prawdziwego sąsiedztwa charakteryzują się zagęszczeniem odpowiednio D1, D2 i D3. Przyjmijmy teraz, że do tego sąsiedztwa wprowadza się nowa osoba. Zgodnie z tym, co pisaliśmy wcześniej, przy danym gradiencie gęstości osoba wybierze taki pierścień, w którym spełnienie jej upodobania do ciszy i zieleni zostanie zrównoważone zaspokojeniem potrzeby dostępu do sklepów i usług publicznych. Oznacza to, że każda osoba staje przed wyborem jednej z trzech wariantowych kombinacji gęstości i odległości od lokalnego centrum:
 
  • Pierścień 1. Gęstość D1 i odległość od sklepów około R1.
  • Pierścień 2. Gęstość D2 i odległość od sklepów około R2.
  • Pierścień 3. Gęstość D3 i odległość od sklepów około R3.
  W takiej sytuacji każda osoba może dokonać innego wyboru w zależności od własnych preferencji dotyczących równowagi między gęstością a odległością od lokalnego centrum. Na potrzeby naszych rozważań wyobraźmy sobie, że wszyscy ludzie w danym sąsiedztwie zostaną poproszeni o dokonanie takiego wyboru (przez chwilę zapomnijmy o rodzaju i liczbie domów dostępnych w danej okolicy). Przypuśćmy, że N1 osób zdecyduje się na pierścień 1., N2 — na pierścień 2., a N3 — na pierścień 3. Ponieważ powierzchnie wszystkich trzech pierścieni są określone i ograniczone, to znając liczbę osób, które wybrały każdy z nich, można obliczyć hipotetyczne gęstości tych obszarów. Innymi słowy, jeżeli w wyobraźni przyporządkujemy ludzi wybranym przez nich pierścieniom, to będziemy mogli wyliczyć hipotetyczne wartości gęstości, które w rezultacie pojawiłyby się na każdym z trzech obszarów.
  Oto stoimy wobec dwóch fascynujących możliwości:
  1. Nowe gęstości różnią się od aktualnych.
  2. Nowe gęstości są takie jak obecne.
  Dużo bardziej prawdopodobny jest pierwszy przypadek. Nie jest to jednak sytuacja stabilna, ponieważ zmienne decyzje będą powodowały zmiany gęstości. Drugi przypadek, którego wystąpienie będzie mniej prawdopodobne, jest bardziej stabilny. Oznacza bowiem, że ludzie, dokonując wolnego wyboru, odtworzą wspólnie ten sam wzór gęstości, w ramach którego dokonywali tego wyboru. A to już jest zasadnicza różnica.
  Jeżeli założymy, że sąsiedztwo o określonej powierzchni całkowitej ma przyjąć pewną liczbę osób (określoną przez średnią gęstość zaludnienia w konkretnym rejonie), to istnieje tylko jedna stabilna konfiguracja gęstości. Opiszemy teraz procedurę obliczeniową, która może być stosowana do określenia tej stabilnej konfiguracji gęstości.
  Zanim wytłumaczymy procedurę obliczeniową, musimy podkreślić, jak ważny, wręcz fundamentalny jest ten rodzaj stabilnej konfiguracji gęstości zaludnienia.
  W dzisiejszym świecie, gdzie gradienty gęstości zazwyczaj nie są stabilne w naszym rozumieniu, większość ludzi jest zmuszona do życia w warunkach, w których punkt równowagi między spokojem a aktywnością nie odpowiada ani ich pragnieniom, ani potrzebom. Wynika to z tego, że całkowita liczba dostępnych domów i mieszkań w różnych odległościach od centrum nie jest wystarczająca. W takiej sytuacji ludzie bogaci, którzy są w stanie zapłacić za to, czego pragną, mogą znaleźć domy i mieszkania ulokowane w wybranym przez siebie punkcie równowagi. Mniej zamożni i biedni mieszkańcy są natomiast zmuszeni zająć to, co pozostało. Wszystko to jest uzasadnione przez klasę średnią ekonomią „renty gruntowej”, zgodnie z którą tereny położone w różnych odległościach od centrum aktywności mają różną wartość, ponieważ więcej lub mniej ludzi chce mieszkać w tych odległościach. Ale w rzeczywistości istnienie zróżnicowania renty gruntowej jest mechanizmem ekonomicznym, który pojawia się w sytuacji niestabilnej konfiguracji gęstości zaludnienia po to, aby tę niestabilność kompensować.
  Chcemy podkreślić, że w sąsiedztwie o stabilnej konfiguracji gęstości (stabilnej w naszym rozumieniu tego słowa) cena gruntu nie musiałaby być zróżnicowana ze względu na odległości od centrum, ponieważ ogólna liczba dostępnych domów w każdym pierścieniu odpowiadałaby dokładnie liczbie ludzi, którzy chcieliby mieszkać w określonej odległości od centrum. Gdyby popyt był równoważny z podażą w każdym pierścieniu, renta gruntowa mogłaby być w każdym pierścieniu jednakowa. Każdy człowiek, bogaty czy biedny, mógłby wówczas zyskać właśnie taką równowagę, jakiej potrzebuje.
  Pora teraz na przedstawienie metody obliczania stabilnej gęstości dla danego sąsiedztwa. Stabilność ta zależy od bardzo subtelnych zmiennych psychologicznych. O ile wiemy, te zmienne nie mogą być przedstawiane za pomocą równań matematycznych w sposób ścisły pod względem psychologicznym. Z tego powodu na razie nie jest możliwe podanie jakiegoś matematycznego modelu stabilnej gęstości. Zamiast tego postanowiliśmy wykorzystać fakt, że każdy człowiek może dokonać wyboru potrzebnej mu równowagi między ciszą i aktywnością. Skonstruowaliśmy prostą grę, w której używamy jednostkowych wyborów i która jest źródłem danych do obliczeń. Dzięki tej grze można uzyskać stabilną konfigurację gęstości w ciągu kilku minut. Ogólnie rzecz biorąc, gra symuluje zachowanie rzeczywistego systemu. Sądzimy, że pozwala ona uzyskać wyniki znacznie bardziej godne zaufania niż jakiekolwiek obliczenia matematyczne.

GRA — GRADIENT GĘSTOŚCI

  1. Narysuj mapę złożoną z trzech koncentrycznych półpierścieni. Niech stworzą półokrąg (jeżeli przyjąłeś argumenty przytoczone we wzorcu EKSCENTRYCZNE JĄDRO (28)) lub pełne koło. Dopasuj półokrąg tak, by się zmieścił w podkowie największej gęstości. Zaznacz centrum półokręgu jako środek tej podkowy.
  2. Jeżeli zewnętrzny promień półokręgu wynosi R, wtedy średnie promienie trzech pierścieni będą równe R1, R2, R3, wynosząc odpowiednio: R1 = R/6; R2 = 3R/6; R3 = 5R/6.
  3. Stwórz planszę do gry, na której będą narysowane te trzy koncentryczne półokręgi. Wyraź wartości promieni, podając liczbę bloków ulicznych, żeby ludzie łatwiej to zrozumieli, na przykład 300 m = 3 bloki ulic.
  4. Zdecyduj, jaka ma być całkowita liczba mieszkańców wybranego dla gry sąsiedztwa. Wybór ten oznacza także ustalenie całkowitej średniej gęstości dla tego obszaru. Nie może on być w sprzeczności z ogólnym wzorem zagęszczenia w tym rejonie. Powiedzmy, że całkowita populacja w rozpatrywanej społeczności składa się z N rodzin.
  5. Znajdź 5 osób, które będą przypominać mieszkańców tej społeczności. Weź pod uwagę: zwyczaje kulturowe, wykształcenie, pochodzenie i tak dalej. Jeżeli to możliwe, należy wybrać dziesięć osób należących do analizowanej społeczności.
  6. Zaprezentuj graczom zestaw zdjęć miejsc, które pozwolą wyobrazić sobie obrazy typowe dla gęstości (w rodzinach na hektar). Umieść te fotografie tak, by gracze widzieli je w czasie gry i mogli korzystać z nich, dokonując swoich wyborów.
  7. Daj każdemu graczowi pionek, który może umieścić na planszy wewnątrz jednego z trzech pierścieni.
  8. Aby rozpocząć grę, określ, jaki procent całkowitej populacji ma się znaleźć w każdym z trzech pierścieni. Nie ma znaczenia to, jaki procent wybierzesz na początku — w toku gry wartości te samoistnie się dostosują. Jednak by nie komplikować zasad, wybierz dla każdego z pierścieni wartości będące wielokrotnością 10%. Na przykład: 10% w pierwszym pierścieniu, 30% w drugim i 60% w trzecim.
  9. Następnie przelicz te wartości procentowe na rzeczywiste gęstości wyrażone w liczbie rodzin na hektar. Ponieważ w czasie gry będziesz musiał robić to wielokrotnie, najlepiej stworzyć tabelę, za pomocą której przeliczysz procenty bezpośrednio na gęstości. Możesz zrobić taką tabelkę, podstawiając wartości N i R wybrane przez ciebie dla twojej społeczności do przedstawionych niżej wzorów. Wzory te opierają się na prostej planimetrii i arytmetyce populacji. R jest wyrażone w setkach metrów, a w przybliżeniu liczbą bloków ulicznych. Gęstość wyrażona jest w liczbie rodzin na hektar. Pomnóż gęstość właściwą dla każdego pierścienia przez liczbę od 1 do 10, odpowiadającą wartości procentowej przyporządkowanej danemu pierścieniowi — jeżeli w trzecim pierścieniu jest to 30%, to gęstość jest trzykrotnie wyższa niż dane początkowe równania (czyli 24N/5πR2).
10%
Pierścień 1.8N/πR2
Pierścień 2.8N/3πR2
Pierścień 3.8N/5πR2
  10. Po obliczeniu właściwych gęstości zapisz je na trzech karteczkach, po czym umieść te karteczki na planszy wewnątrz odpowiadających im pierścieni.
  11. Karteczki definiują tymczasową konfigurację gęstości dla tej społeczności. Każdy pierścień znajduje się w pewnej typowej odległości od centrum i charakteryzuje go też pewna gęstość. Poproś graczy, aby uważnie przyjrzeli się zdjęciom przedstawiającym gęstości zaludnienia odpowiadające pierścieniom, a następnie zdecydowali, w którym z trzech pierścieni zostałaby zrównoważona ich potrzeba ciszy i zieleni z potrzebą dostępu do sklepów. Poproś każdą z osób uczestniczących w grze, aby umieściła swój pionek w pierścieniu, na który się zdecydowała.
  12. Kiedy każdy z dziesięciu pionków znajdzie się na planszy, ich rozkład zdefiniuje nowe rozmieszczenie populacji. Najprawdopodobniej różni się ono od tego, z którym zaczynaliście grę. Oblicz nowy układ wartości procentowych; niech będą to wartości uśrednione między początkowo przyjętymi przez ciebie a tymi, które wynikają z układu pionków graczy na planszy. Zaokrąglij otrzymane wartości do 10%. Poniżej podano przykład takich obliczeń:
Uprzednie wartości procentowePionki graczy Nowe wartości procentowe
10%3 = 30%→20%
20%4 = 40%→30%
30%3 = 30%→50%
  Jak widać, nowe wartości nie są dokładnie wartościami uśrednionymi, ale odpowiadają wartości średniej na tyle, na ile jest to możliwe. Nadal są wielokrotnościami dziesięciu.
  13. Teraz powtarzaj etapy opisane w punktach od 9. do 12. dopóty, dopóki wartości procentowe wynikające z ułożenia pionków przez graczy nie będą równe zdefiniowanym przez ciebie na początku danej rundy. Gdy przeliczysz ostatnią wartość procentową na gęstość, to znalazłeś stabilną konfigurację gęstości dla rozpatrywanej społeczności. Skończ grę i napijcie się czegoś dla uczczenia sukcesu.
  Na podstawie przeprowadzonych prób zauważyliśmy, że gra bardzo szybko osiąga stan stabilności. Dziesięć osób w kilka minut może zdefiniować stabilny rozkład gęstości. W poniższej tabeli zaprezentowaliśmy wyniki z serii gier.
STABILNE ROZMIESZCZENIE GĘSTOŚCI DLA SPOŁECZNOŚCI O RÓŻNYCH ROZMIARACH
Wartości te są odpowiednie przy założeniu, że kształt obszaru zamieszkanego przez daną społeczność jest półokręgiem.
Promień (w liczbie bloków ulicznych)Populacja (w liczbie rodzin)Gęstość (liczba rodzin na akr)
Pierścień 1.Pierścień 2.Pierścień 3.
21501595
3150752
33002175
4300732
46002974
66001542
612003693
912001851
  Koniecznie trzeba zdawać sobie sprawę z tego, że nierozsądne byłoby bezpośrednie wykorzystanie podanych w tabeli wartości. Liczby będą bowiem zależeć od konkretnego rozkładu danego sąsiedztwa i od uwarunkowań kulturowych różnych podkultur. Dlatego też uważamy, że niezwykle istotne jest, by ci mieszkańcy danej społeczności, którzy chcą zastosować wzorzec PIERŚCIENIE GĘSTOŚCI (29), sami zagrali w tę grę. W ten sposób będą mogli wyznaczyć stabilny gradient gęstości, dostosowany do ich własnej sytuacji. Liczby przytoczone wyżej mają jedynie zilustrować nasze rozważania.
  Dlatego:
  Gdy znasz już dokładną lokalizację centrum społeczności, zdefiniuj pierścienie obniżającej się lokalnej gęstości zabudowy mieszkaniowej wokół centrum. Jeżeli nie masz innego wyjścia, wybierz gęstości z powyższej tabeli. Będzie jednak dużo lepiej, jeśli przeprowadzisz badania gradientu gęstości, grając w opisaną wyżej grę. W ten sposób wyznaczysz wartości zgodne z intuicją ludzi, którzy będą należeć do danej społeczności.

***

  W obrębie poszczególnych pierścieni zagęszczenia zaludnienia zachęcaj ludzi, by budowali domy, tworząc skupiska mieszkalne — samorządne spółdzielnie składające się z 8—15 gospodarstw domowych różnego rozmiaru w zależności od zagęszczenia — GRUPA DOMÓW (37). Uwzględniaj zagęszczenie zaludnienia w pierścieniach, konstruując domy wolno stojące — GRUPA DOMÓW (37), DOMY SZEREGOWE (38), lub skupiska domów mieszkalnych o większym zagęszczeniu — GÓRKA MIESZKALNA (39). Miejsca publiczne — PROMENADA (31), PUBLICZNE PLACYKI (61) — planuj na tych terenach, które mają już wystarczające zagęszczenie zaludnienia, by mogły dobrze funkcjonować — INTENSYWNOŚĆ RUCHU PIESZEGO (123).
An unhandled error has occurred. Reload 🗙